Forhold
Forholdet mellom to tall er svaret vi får når vi deler tallene på hverandre.
Hvis vi kaller tallene for og , så er forholdet mellom og lik brøken .

Som du ser av definisjonen ovenfor, er forhold i matematikken noe ganske annet enn forholdet til vennene dine.
Forholdet mellom tallene og er .
Forholdet mellom tallene og er .
Vi støter ofte på forhold i matematikken. Vi skal gi noen eksempler på dette, og også se på hvordan vi kan regne med forhold.
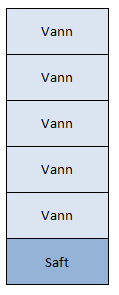
Vi skal blande saft og vann. På saftflasken står det oppgitt at blandingsforholdet er . Det vil si at for hver del saft skal vi ha 5 deler vann.
Til for eksempel 3 liter ren saft trenger vi liter vann. Det gir 3 liter pluss 15 liter som er 18 liter «saft og vann».
Til 10 liter vann trenger vi liter ren saft. Det gir 10 liter pluss 2 liter som er 12 liter «saft og vann».
Men hvor mye ren saft trenger vi for å lage 21 liter «saft og vann»?
Vi må tenke oss at saftblandingen består av 6 deler, hvorav 1 del er ren saft, og 5 deler er vann.
Hver del består av liter. Ren saft utgjør 1 del av blandingen, og da trenger vi altså liter ren saft.
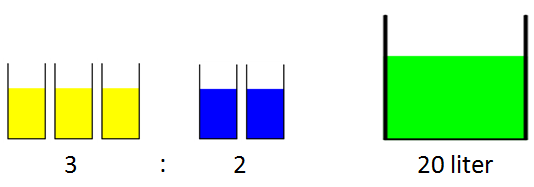

Anders blander gul og blå maling i forholdet for å få grønn maling. Han får til sammen 20 liter grønn maling.
Hvor mye gul maling og hvor mye blå maling har han brukt?
3 deler gul maling pluss 2 deler blå maling gir 5 deler. Disse 5 delene tilsvarer 20 liter.
Hver del tilsvarer da
Det er 3 deler gul maling som tilsvarer .
Det er 2 deler blå maling som tilsvarer .
Han har brukt 12 liter gul maling og 8 liter blå maling.
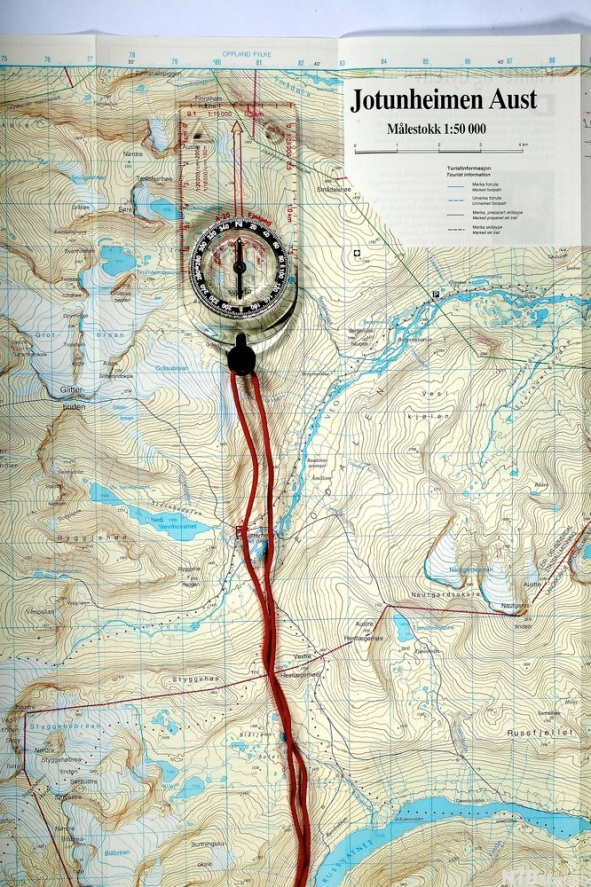
Et kart har målestokken 1 : 50 000.
Det vil si at 1 cm på kartet svarer til 50 000 cm i terrenget. Det betyr at forholdet mellom avstander på kartet og avstander i terrenget er .
Når vi går fra kartet til terrenget, må vi multiplisere med 50 000. Husk at terrenget er større enn kartet.
cm på kartet svarer til
i terrenget.
Når vi går fra terrenget til kartet, må vi dividere med 50 000. Husk at kartet er mindre enn terrenget.
km i terrenget svarer til
på kartet.
Valutakurser viser forholdet mellom verdien på ulike valutaer.
Tabellen nedenfor viser verdien av ulike utenlandske valutaer gitt i norske kroner 10.11.2012.
Valuta | 100 DKK | 100 SEK | 1 EUR | 1 GBP | 1 USD |
|---|---|---|---|---|---|
Verdi i NOK | 97,4 | 84,9 | 7,279 | 9,125 | 5,72 |

Vi ser at 1 USD (amerikansk dollar) koster norske kroner, NOK.
Da vil 20 USD koste .
100 DKK (danske kroner) koster 97,4 NOK.
Det vil si at 1 DKK koster .
20 DKK vil da koste .
Vi går altså «veien om 1».
Når vi skal gå motsatt vei, må vi dividere på «prisen for 1».
For 80 NOK får vi .
For 80 NOK får vi .
Dette er helt tilsvarende regningsmåte som ved kjøp av for eksempel epler. Hvis prisen for én kg epler er 14 kroner, så må vi for 4 kg epler betale . Tilsvarende får vi for 49 kroner

Vi ser en person avbildet ved siden av en mur som vi fra før av kjenner høyden til. Kan vi da beregne høyden til personen ut fra bildet?
Vi vet at muren i virkeligheten er m høy. Vi måler så høyden til muren på bildet og finner at den er 7 cm.
Da kan vi regne ut forholdet mellom virkelige høyder og høyder på bildet til
.
Vi måler så høyden til personen på bildet til 3 cm.
Personens høyde er i virkeligheten lik