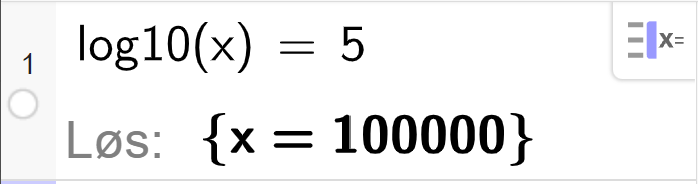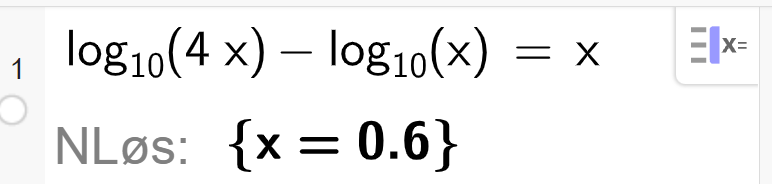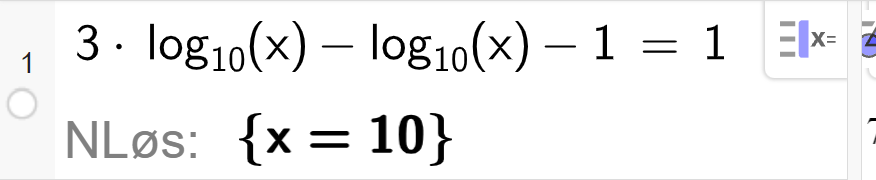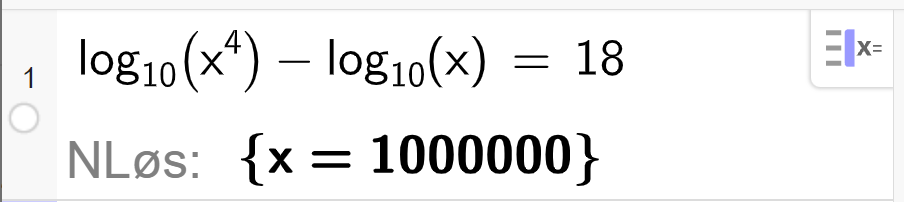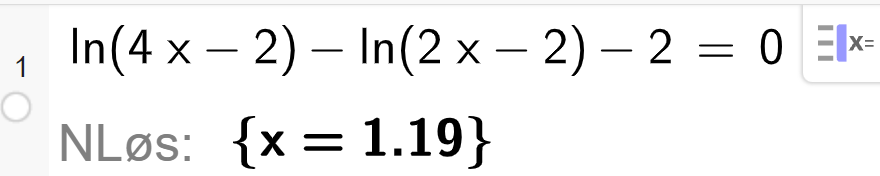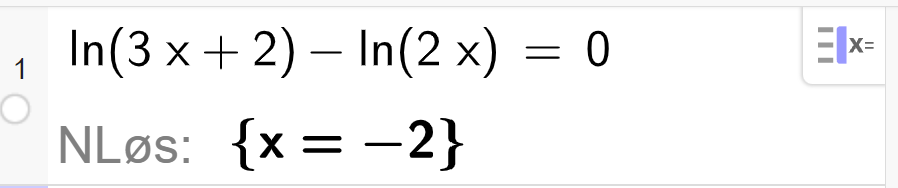Logaritme- og eksponentiallikninger
Løs likningene ved regning og med CAS. Husk parentes når du bruker CAS.
a)
Løsning
Løst med CAS:
b)
Løsning
Løst med CAS:
c)
Løsning
Løst med CAS:
d)
e)
f)
g)
h)
a) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
b) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
c) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS (merk at vi bare får med én av løsningene):
d) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
e) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
f) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
g) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
h) Vi har gitt likningen
1) For hvilke verdier av
2) Løs likningen ved regning.
3) Løs likningen med CAS.
Løsning
Løsning med CAS:
Løs likningene.
a)
b)
c)
d)
e)
Løs likningene.
a)
b)
c)
d)
Løs likningene. Husk at logaritmer bare er definert for positive tall.
a)
b)
c)
d)
e)
f)
g)
h)
Vurder løsningsforslagene og diskuter hva elevene har tenkt. Hvilke logaritmeregler må man bruke? Klarer du å lage et bedre løsningsforslag? Oppgaven egner seg fint for diskusjon i små grupper.