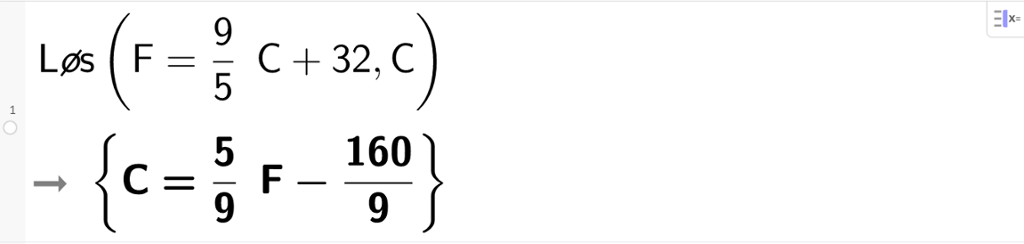Formelregning
Hjemmebanen til Liverpool FC heter Anfield Stadium, eller bare Anfield. Banestørrelsen er 100 meter x 69 meter.
a) Hva slags geometrisk figur er en fotballbane? Skriv opp formelen vi bruker for å regne ut arealet av en slik figur.
b) Hvor mange kvadratmeter er Anfield?
Old Trafford er hjemmebanen til Manchester United. Banestørrelsen er 106 meter x 69 meter.
c) Hvor mange kvadratmeter større er banen til Manchester United enn banen til Liverpool FC?
Grunnflaten til en normalt stor enebolig er 100 m2.
d) Hvor mange eneboliger av denne størrelsen er det plass til på hvert av stadionene?
Ellen hadde på 2000-tallet et såkalt kontantkort på mobilen. Det kostet 0,59 kr for en tekstmelding. La A stå for antall tekstmeldinger og x for hvor mye penger det er på kontantkortet.
a) Finn en formel for antall meldinger hun kan sende for pengene som er på kortet.
b) Hvor mange tekstmeldinger kan Ellen sende dersom hun har 150 kr igjen på kontantkortet?
Løs oppgavene uten hjelpemidler.
Gitt formelen
a) farten, v
b) tiden, t
Løs oppgavene uten hjelpemidler.
a) Arealet av en sirkel er gitt ved formelen
Løs formelen med hensyn på r.
b) Volumet av en terning er gitt ved formelen
Løs formelen med hensyn på s.
c) Volumet av en sylinder er gitt ved
1) Løs formelen med hensyn på h.
2) Løs formelen med hensyn på r.
d) Volumet av en kjegle er gitt ved
1) Løs formelen med hensyn på h.
2) Løs formelen med hensyn på r.
e) Volumet av en kule er gitt ved
Løs formelen med hensyn på r.
Løs oppgavene uten hjelpemidler.
Fra fysikken har vi disse formlene.
Løs formlene med hensyn på t.
a)
b)
c)
Løs oppgavene med hjelpemidler.
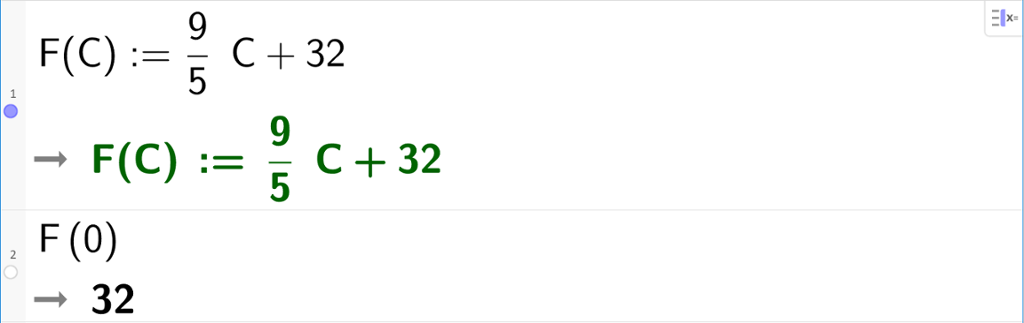
Sammenhengen mellom fahrenheitgrader og celsiusgrader er gitt ved formelen
Her står C for temperaturen målt i celsiusgrader og F for temperaturen målt i fahrenheitgrader.
a) Gradestokken viser en dag
b) Løs formelen med hensyn på C.
c) Gradestokken viser 65°F. Hvor mange grader celsius tilsvarer dette?
Løs oppgavene med hjelpemidler.
Et telefonabonnement kostet i 2008 49 kroner i fast månedspris og 0,85 kroner per minutt for samtaler. Et annet abonnement kostet 99 kroner i fast månedspris og 0,59 kroner per minutt for samtaler.
Ved hvor mange minutter ringetid er de to abonnementene likeverdige i pris?
Løs oppgavene uten hjelpemidler.
Vinkelsummen i en trekant er 180°, i en firkant 360°, og i en femkant 540° .
a) Lag en formel som viser vinkelsummen V i en mangekant med n sider.
I en regulær mangekant er vinklene like store, for eksempel er vinklene i en regulær trekant 60°, i en regulær firkant 90° og i en regulær femkant 108°.
b) Finn en formel som viser vinkelen i en regulær
Hva kan du om formelregning?
Filer
- Formelregning(DOCX)
- Formelregning(PDF)