Definisjon og måleenheter for areal

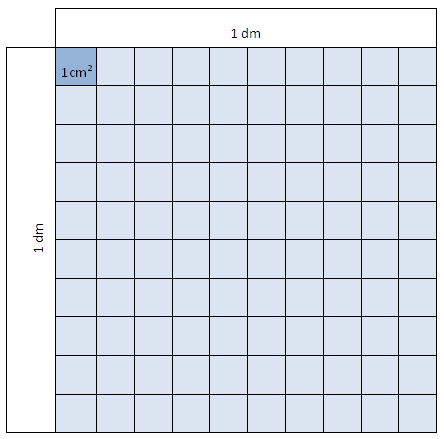
Vi definerer én kvadratdesimeter, 1 dm², som arealet, eller flateinnholdet, til et kvadrat med sidelengder på 1 dm.

Et kvadrat med sider 1 cm har et areal på én kvadratcentimeter, 1 cm².

Tilsvarende definerer vi arealer på 1 m², 1 mm² osv.

Figuren viser at 1 dm² tilsvarer
100 cm². Det betyr igjen at

$1 {\mathrm{cm}}^2=\frac{1}{100}{\mathrm{dm}}^2=0,01 {\mathrm{dm}}^2$

Vi husker sammenhengen mellom måleenheter for lengde:

$1 \mathrm{m}=10 \mathrm{dm} 1 \mathrm{dm}=10 \mathrm{cm} 1 \mathrm{cm}=10 \mathrm{mm}$

$\begin{array}{rcl}2,3 \mathrm{m}& = & 23 \mathrm{dm}=2300 \mathrm{mm}\\ & & \\ 450 \mathrm{cm}& =& 4,50 \mathrm{m}\end{array}$

Når vi setter opp måleenhetene etter hverandre som i tabellen nedenfor, kan vi ha som huskeregel at vi må gange med 10 når vi går én plass til høyre i tabellen (flytte komma én plass til høyre), og dele med 10 når vi går én plass til venstre (flytte komma én plass til venstre).

$\begin{array}{rcl}2,3 {\mathrm{dm}}^2& = & 230 {\mathrm{cm}}^2=23 000 {\mathrm{mm}}^2\\ & & \\ 450 {\mathrm{cm}}^2& =& 0,0450 {\mathrm{m}}^2\end{array}$

Når vi setter opp måleenhetene for areal etter hverandre som i tabellen nedenfor, kan vi ha som huskeregel at vi må gange med 100 når vi går én plass til høyre i tabellen (flytte komma to plasser til høyre), og dele med 100 når vi går én plass til venstre (flytte komma to plasser til venstre).

For større arealer har vi også noen andre måleenheter

$\begin{array}{rcl}1 \mathrm{a} & =& 100 {\mathrm{m}}^2 \left(\mathrm{ar}\right)\\ 1 \mathrm{da} & =& 1 \mathrm{mål}=10 \mathrm{a}=1 000 {\mathrm{m}}^2 \left(\mathrm{dekar}\right)\\ 1 \mathrm{ha} & =& 100 \mathrm{a}=10 000 {\mathrm{m}}^2 \left(\mathrm{hektar}\right)\\ 1 {\mathrm{km}}^2 & =& 1 000 \mathrm{da}=1 000 000 {\mathrm{m}}^2 \left(\mathrm{kvadratkilometer}\right)\end{array}$