Smittespredning – modeller
De fleste land kom fram til at drastiske tiltak måtte iverksettes, selv om det betydde store endringer i hverdagen til innbyggerne. For å hindre smittespredning ble alle offentlige og private bedrifter stengt ned, og kommunikasjon mellom mennesker måtte foregå over nettet. Norge var et av disse landene.

Andre land valgte en annen strategi og lot smitten spre seg mer eller mindre ukontrollert uten store inngrep, i håp om at flokkimmunitet ville stoppe spredningen på en effektiv måte. Sverige var et av disse.
Hva er den beste løsningen?
Valgene de ulike landene tok, baserte seg på råd fra eksperter innen smittespredning og på ny kunnskap om selve viruset. Men også andre hensyn ble tatt med i vurderingen. Det var spesielt påvirkningen på samfunnsøkonomien som ble drøftet. Uansett hvilke løsninger som ble valgt, medførte de både fordeler og ulemper.
Stengte samfunn

Fordelene ved å stenge ned samfunnet er at få mennesker blir smittet, helsevesenet har nok kapasitet, og det blir få dødsfall. Ulempene er bedrifter som sliter, mange permitterte, hjemmeskole, minimal sosial omgang og at størstedelen av befolkningen fremdeles er sårbare for smitte. For at denne strategien skal virke på sikt, må det utvikles vaksiner. Mennesker som er vaksinert, vil være beskyttet mot dette viruset, og de smitter heller ikke andre.
Flokkimmunitet gjennom sykdom eller vaksine
De som har vært gjennom en covid-19-infeksjon, opparbeider immunitet som beskytter mot ny smitte av dette viruset så lenge immuniteten varer, på samme måte som vaksinen mot samme virus virker. Hvis mange mennesker får sykdommen og blir immune, vil befolkningen oppnå flokkimmunitet. Ulempen er at noen blir svært syke og mange dør.
To andre momenter vi må ta med i vurderingen, er at immunitet kan ha begrenset varighet, og at virus muterer hyppig. De som har oppnådd immunitet gjennom sykdom eller gjennom vaksinering, kan bli utsatt for ny smitte senere.
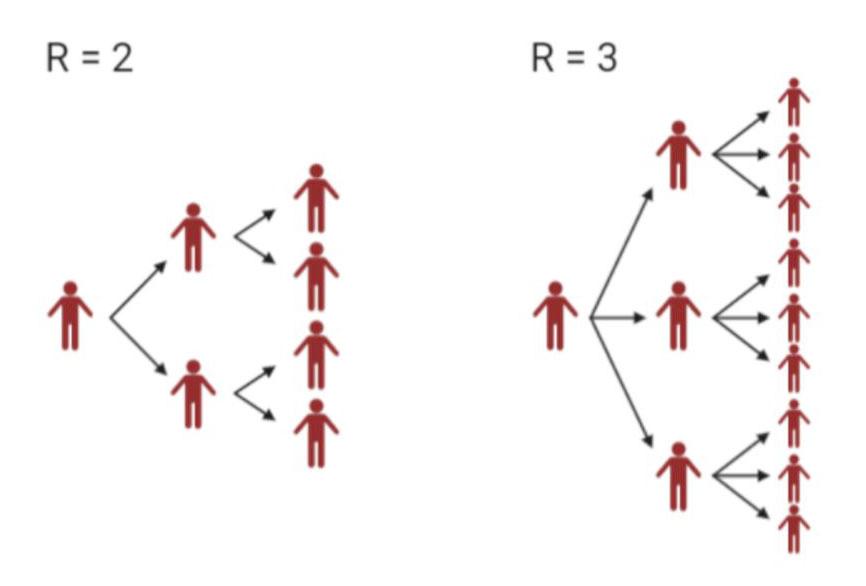
Vi skal nå lage et program som simulerer hvordan smitteutviklingen kan foregå. Realistiske modeller blir fort veldig kompliserte, så i vårt program bruker vi bare det såkalte R-tallet for å finne smittede personer. R-tallet sier oss hvor mange personer en syk person smitter videre.
Under finner du et program der du kan justere følgende verdier:
R-tallet ved starten av utbruddet
hvor mange uker det tar før tiltak iverksettes
hva R-verdien blir etter at tiltakene er iverksatt
hvor mange uker denne R-verdien varer
I starten vil R-tallet ofte være over 1, og etter at man har iverksatt tiltak, bør det helst være under 1. Prøv deg fram med ulike verdier.
Hva må R-tallet være for at antall smittede skal gå ned?
Obs! Bruk punktum (.) i stedet for komma (,) hvis du velger desimaltall som R-tall.
Tiltak som å stenge ned hele samfunnet kan ikke fortsette i det uendelige. Før eller siden må vi begynne å gå tilbake til hverdagen. I Norge ble det lettet på en del tiltak før en vaksine var ferdigutviklet. Det kan derfor være interessant å utvide programmet til å ha flere enn to faser. Prøv å gjøre det selv: Utvid programmet slik at det kan legges inn faser med varierende R-tall. Det kan være lurt å bruke ei while-løkke, slik at brukeren kan be om flere perioder for hver kjøring.
Eksperimenter med R-tall mellom 1 og 4, og bruk for eksempel et intervall på 5 uker mellom hver gang restriksjonene endres.
Programmet ditt er ikke feil selv om det står "1e…" øverst i grafen. Siden det er en del smittede personer i befolkningen, og siden veksten er eksponentiell, vil smittetallet fort eksplodere. Ved svært høye smittetall markeres grafen øverst med "1e" etterfulgt av et tall (f.eks. 1e8, som betyr ). Tallet viser altså hvor mange null det skal være etter verdiene på y-aksen.
Begrensende faktorer

Heldigvis er det i virkeligheten en del faktorer som vil begrense smittespredningen. Immunitet har vi allerede nevnt. I tillegg trenger ikke politikerne å vedta tiltak lang tid i forveien. Ser de at ting er i ferd med å komme ut av kontroll, kan de iverksette tiltak på kort varsel.
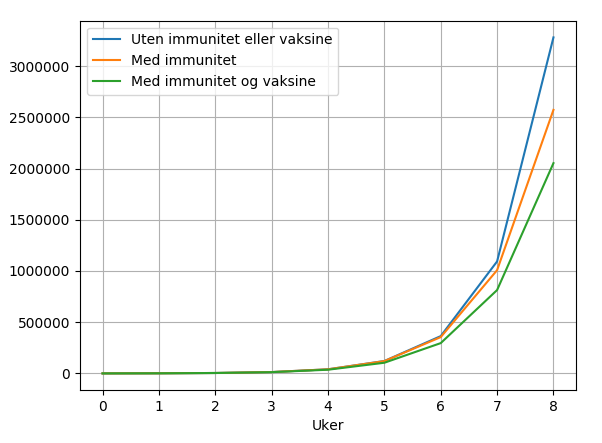
Modellen vår er relativt enkel, men gir forhåpentligvis en viss forståelse av hvordan smitte sprer seg. Skal vi få en mer realistisk modell, må vi legge inn noen flere faktorer: De syke blir friske og kan ikke smitte andre. De blir dessuten immune og kan ikke bli syke en gang til. Vaksiner utvikles og gis til befolkningen. De vaksinerte kan ikke bli syke og derfor heller ikke smitte noen.
Programmet under ser på utviklingen i Norges befolkning og simulerer det totale antallet nordmenn som har vært syke. Tre kurver genereres: én for hver av de ovennevnte faktorene vi tar med i beregningene.
Et realistisk tall for antall vaksinasjoner per uke er rundt 200 000. Da vil hele Norges befolkning bli vaksinert i løpet av omtrent et halvt år. Prøv å kjøre simuleringen med ulike R-verdier, og se hva som skjer.
Hvorfor er det viktig at samfunnet klarer å holde R-tallet lavt fram til alle er vaksinerte?
Hvorfor flater immunitetskurven ut før alle er blitt syke?
Hvordan varierer immunitetskurven med R-tallet?
Mer om flokkimmunitet hos Norsk Helseinformatikk
Related content
I dette spillet har du rollen som smittevernansvarlig i Kongsland. Det oppstår et smitteutbrudd, og spørsmålet blir: Kan du stoppe smitten?