Fagartikkel

Volum og overflate av sylinder

Vi har greie formler for volum og overflate av sylindre.

Figuren viser en sylinder. Grunnflaten er en sirkel, og sylinderen er rett når høyden fra sentrum i toppflaten treffer sentrum i grunnflaten.

Her er også volumet lik $G \cdot h$ . Det betyr at

$V = π r^{2} \cdot h$

For å finne overflaten må vi tenke oss sylinderen klippet opp og lagt ut slik tegningen viser. Topp og bunn gir to sirkler, og sideflaten gir et rektangel med grunnlinje lik omkretsen til sirklene.

Formler for volum og overflateareal til en sylinder med høyde $h$ og $r$ som radius i grunnflaten.

$V = π r^{2} \cdot h, O = 2 \cdot π r^{2} + 2 π r \cdot h$

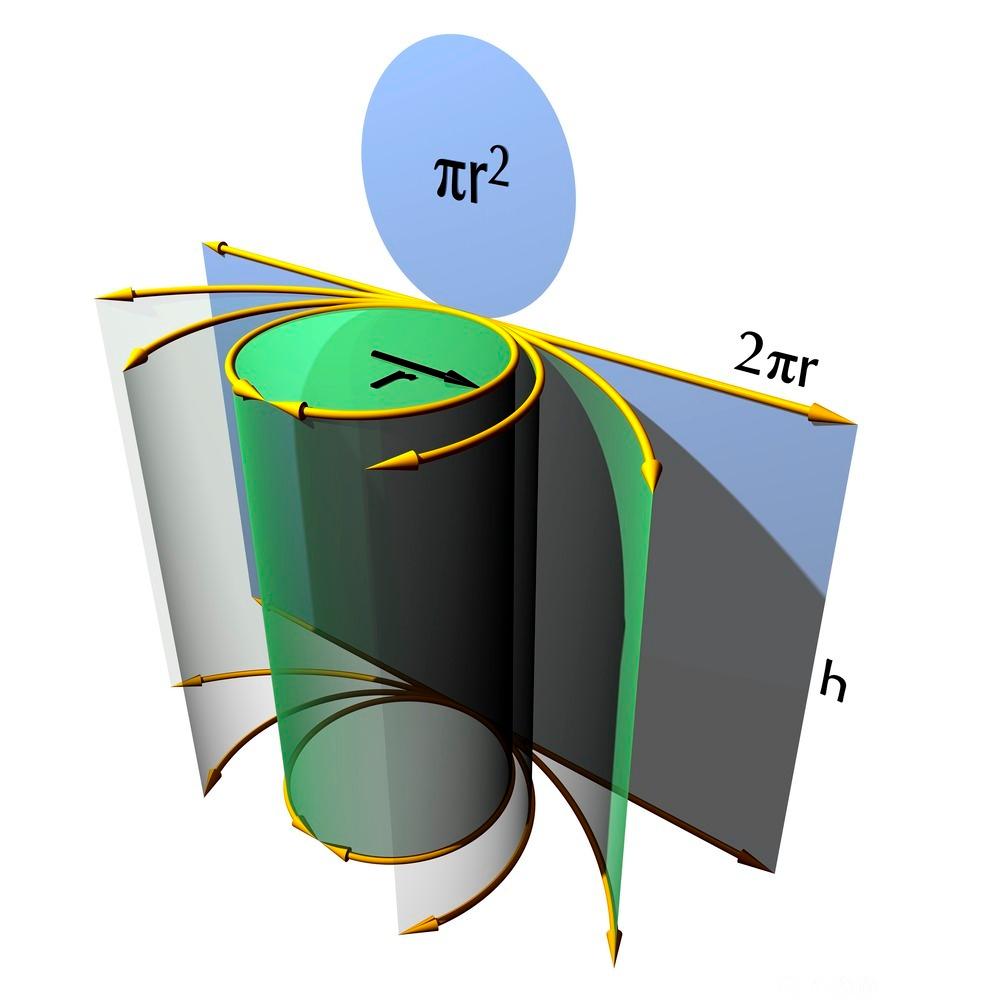
Areal av en sylinder. Illustrasjon. — Image: Science Photo Library, NTB scanpix / CC BY-NC-SA 4.0

Eksempel

I en sylinderformet kakeboks er diameteren i grunnflaten $d = 25, 4 cm$ og høyden $h = 11, 2 cm$ .

Regne ut volum av sylinder i GeoGebra. Bilde. — Image: Olav Kristensen, Stein Aanensen / CC BY-NC-SA 4.0

Volumet blir

$\begin{array}{rcl} V & = & G \cdot h = π r^{2} h \\ = & π \cdot {(\frac{25, 4 cm}{2})}^{2} \cdot 11, 2 cm \\ = & 5 680 {cm}^{3} \\ = & 5, 68 {dm}^{3} \\ = & 5, 68 L \end{array}$

Overflaten består av topp og bunn som er sirkelformet og en rektangulær sideflate.

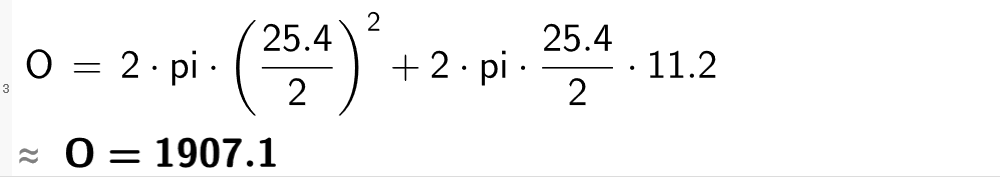
Regne ut overflaten til en sylinder i GeoGebra. Bilde. — Image: Olav Kristensen, Stein Aanensen / CC BY-NC-SA 4.0

Arealet til overflaten blir

$\begin{array}{rcl} O & = & 2 \cdot π r^{2} + 2 π r \cdot h \\ = & 2 \cdot π \cdot {(\frac{25, 4 cm}{2})}^{2} \\ + 2 \cdot π \cdot \frac{25, 4 cm}{2} \cdot 11, 2 cm \\ = & 1 910 {cm}^{2} \end{array}$

Eksempel

Rules for use of text "Volum og overflate av sylinder"