Likningen til ei rett linje
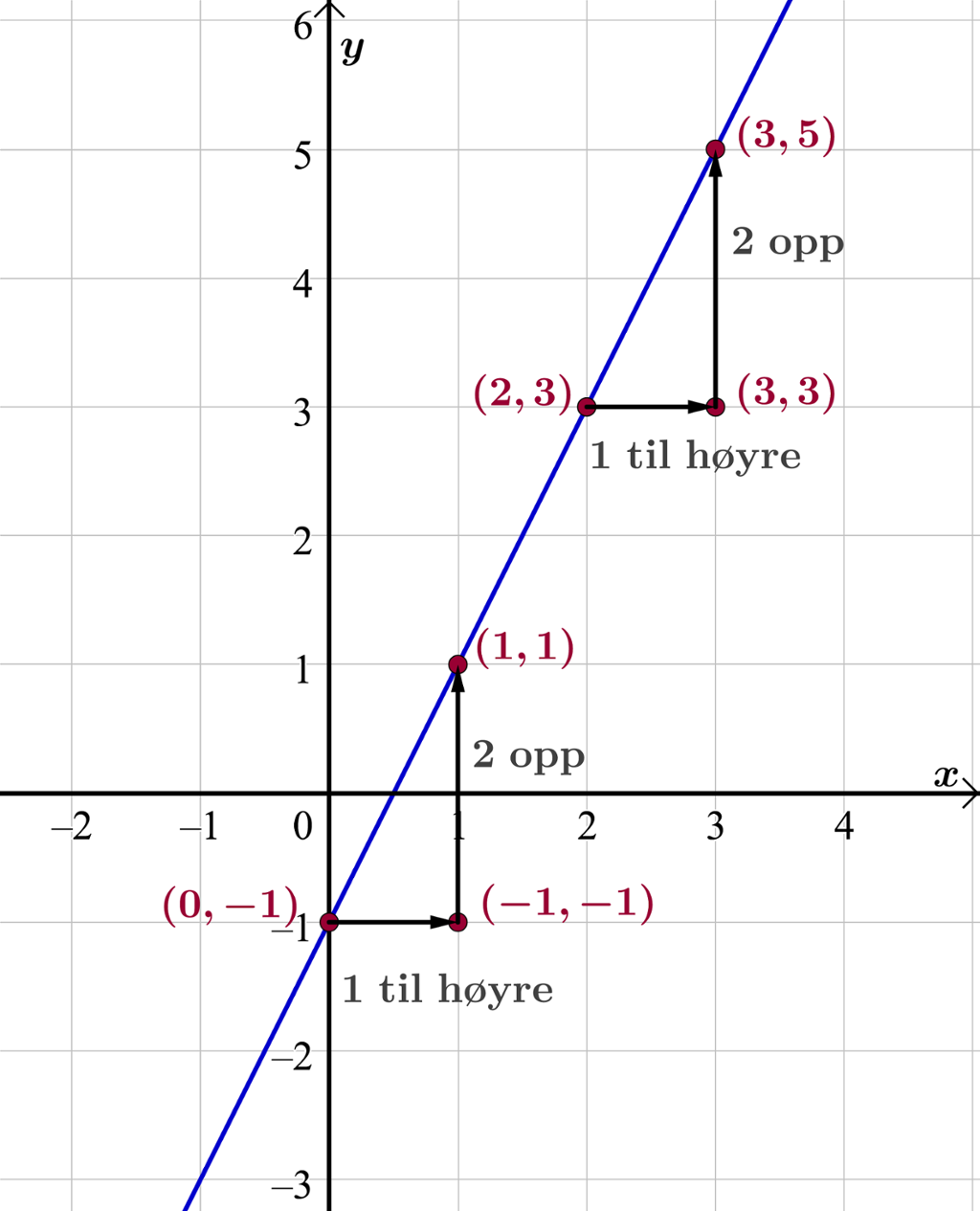
I koordinatsystemet har vi tegnet grafen til en lineær funksjon. Grafen skjærer y-aksen i punktet
Legg merke til at vi like gjerne kan ta utgangspunkt i et annet punkt på grafen for å finne stigningstallet. Vi ser av grafen at vi får samme resultat om vi tar utgangspunkt i punktet (2, 3).
Vi ser på et eksempel der vi skal finne funksjonsuttrykket til ei linje som går gjennom punktet (2, 3) og har stigningstall lik 3. Vi har at det generelle uttrykket for ei rett linje er
Vi kan nå sette punktet (2, 3) inn for x og y:
Vi har nå funnet konstantleddet og har fått følgende funksjonsuttrykk:
Vi kan gå rett på å finne likningen for ei rett linje ved hjelp av det vi kaller ettpunktsformelen.
Vi antar at vi kjenner ett punkt på ei rett linje, og i tillegg kjenner vi stigningstallet til linja. Vi kaller det kjente punktet for
Vi ønsker å finne likningen for linja.
La
Vi multipliserer med nevneren
Dette kan vi snu på og får da
Denne formelen kalles ettpunktsformelen for den rette linja.
Eksempel
Vi kan bruke denne formelen til å finne funksjonsuttrykket til ei linje som går gjennom punktene (2, 4) og (4, 8).
Vi trenger å kjenne stigningstallet til linja for å bruke ettpunktsformelen, så vi regner ut det først:
Nå velger vi ett av punktene vi har fått oppgitt. Vi velger (2, 4) og setter det inn i ettpunktsformelen sammen med stigningstallet:
Funksjonsuttrykket for linja som går gjennom punktene (2, 4) og (4, 8), er altså