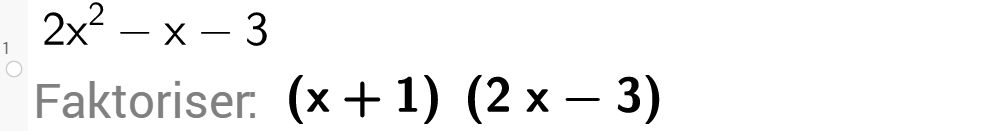Faktorisering av andregradsuttrykk ved hjelp av nullpunktmetoden
Fagstoff
Fagartikkel
Vi viser at nullpunktmetoden alltid kan brukes for å faktorisere andregradsuttrykk.
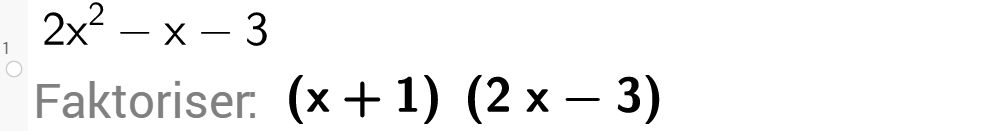
Vi viser at nullpunktmetoden alltid kan brukes for å faktorisere andregradsuttrykk.