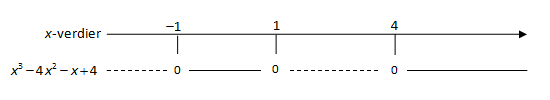Ulikheter av tredje grad
Fagstoff
Fagartikkel
Her viser vi at vi løser ulikheter av tredje grad på tilsvarende måte som ulikheter av andre grad.
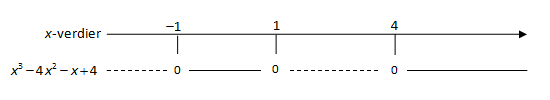
Åpne i fag:
Her viser vi at vi løser ulikheter av tredje grad på tilsvarende måte som ulikheter av andre grad.