Rasjonale uttrykk som inneholder tredjegradspolynomer
Fagstoff
Fagartikkel
Her viser vi hvordan vi kan forenkle rasjonale uttrykk som inneholder tredjegradspolynomer.
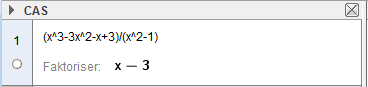
Åpne i fag:
Her viser vi hvordan vi kan forenkle rasjonale uttrykk som inneholder tredjegradspolynomer.
