Gruppert datamateriale. Histogram
Fagstoff
Fagartikkel
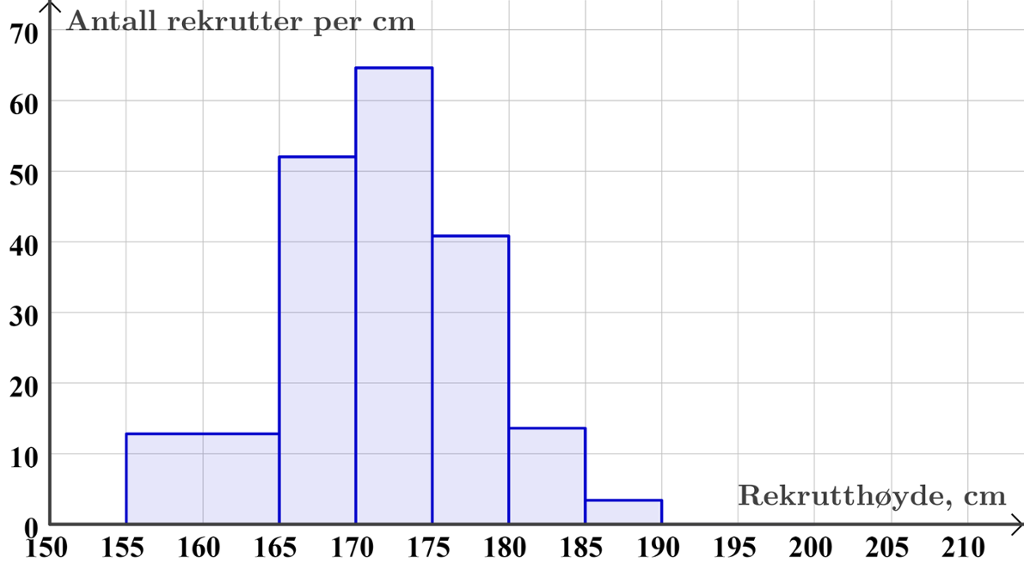
Dersom en frekvenstabell blir veldig stor, deler vi tallmaterialet inn i grupper eller klasser.
Åpne i fag:
Dersom en frekvenstabell blir veldig stor, deler vi tallmaterialet inn i grupper eller klasser.
