Pytagoras’ setning
Fagstoff
Fagartikkel
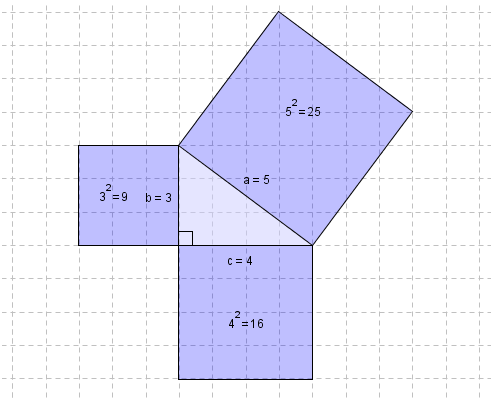
Her ser vi på Pytagoras`setning, som handler om sammenhengen mellom sidene i rettvinklede trekanter.
Åpne i fag:
- Matematikk 1T-Y - TP
- Matematikk 1T-Y - RM
- Matematikk 1T
- Matematikk 1T-Y - NA
- Matematikk 1T-Y - HS
- Matematikk 1P-Y - IM
- Matematikk 1P-Y - NA
- Matematikk 1T-Y - EL
- Matematikk 1T-Y - IM
- Matematikk 1T-Y - DT
- Matematikk 1P-Y - BA
- Matematikk 1P-Y - FD
- Matematikk 1T-Y - BA
- Matematikk 1P-Y - TP
- Matematikk 1T-Y - SR
- Matematikk 1P-Y - DT
- Matematikk 1P-Y - EL
- Matematikk 1T-Y - FD