Drøfting av polynomfunksjonar
Fagstoff
Fagartikkel
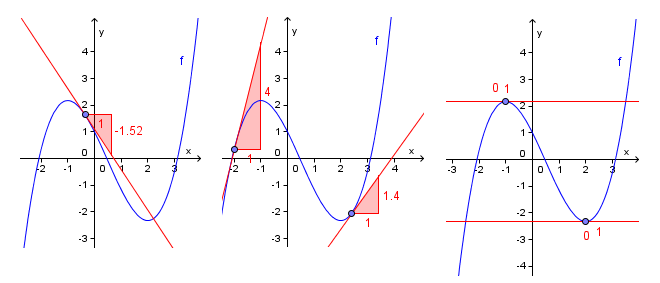
Her bruker vi den deriverte til å finne topp- og botnpunkt på grafen til ein funksjon og til å bestemme der grafen stig og søkk.
Opne i fag:
Her bruker vi den deriverte til å finne topp- og botnpunkt på grafen til ein funksjon og til å bestemme der grafen stig og søkk.
