Funksjonar representerte ved grafar og verditabellar. Verdimengd
Fagstoff
Fagartikkel
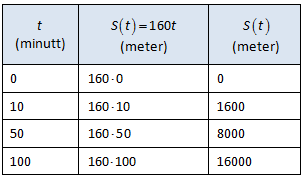
Funksjonar kan representerast ved grafar og verditabellar i tillegg til formlar.
Opne i fag:
- Matematikk 1T
- Matematikk 1P-Y - HS
- Matematikk 1P-Y - SR
- Matematikk 1P-Y - DT
- Matematikk 1T-Y - FD
- Matematikk 1T-Y - TP
- Matematikk 1T-Y - IM
- Matematikk 1P-Y - NA
- Matematikk 1P-Y - TP
- Matematikk 1P
- Matematikk 1P-Y - IM
- Matematikk 1T-Y - NA
- Matematikk 1P-Y - BA
- Matematikk 1P-Y - FD
- Matematikk 1T-Y - SR
- Matematikk 1P-Y - EL
- Matematikk 1T-Y - EL
- Matematikk 2P-Y
- Matematikk 1T-Y - DT
- Matematikk 1T-Y - BA
- Matematikk 1T-Y - HS
- Matematikk 1P-Y - RM
- Matematikk 1T-Y - RM