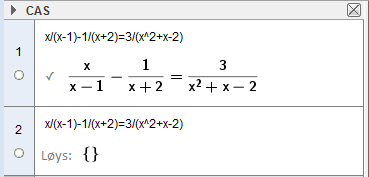Likningar med rasjonale uttrykk
Fagstoff
Fagartikkel
Slik kan vi løyse likningar som inneheld rasjonale uttrykk, dvs. brøkar med den ukjende i nemnaren i ein brøk.
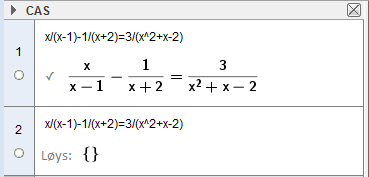
Slik kan vi løyse likningar som inneheld rasjonale uttrykk, dvs. brøkar med den ukjende i nemnaren i ein brøk.