Faktorisering av andregradsuttrykk ved å lage fullstendige kvadrat
Fagstoff
Fagartikkel
Vi ser på kva eit fullstendig kvadrat er, og korleis vi kan faktorisere andregradsuttrykk ved å lage fullstendige kvadrat.
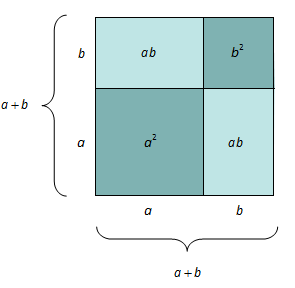
Vi ser på kva eit fullstendig kvadrat er, og korleis vi kan faktorisere andregradsuttrykk ved å lage fullstendige kvadrat.
