Introduksjon til andregradsfunksjonar som modellar
Fagstoff
Fagartikkel
I lineære funksjonar opptrer variabelen x berre i første potens. Her skal vi sjå på funksjonar der x opptrer i andre potens.
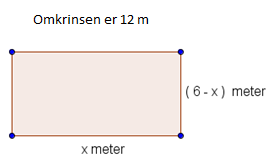
I lineære funksjonar opptrer variabelen x berre i første potens. Her skal vi sjå på funksjonar der x opptrer i andre potens.
