Bruk av formlikskap for å rekne ut ukjende sider i trekantar
Fagstoff
Fagartikkel
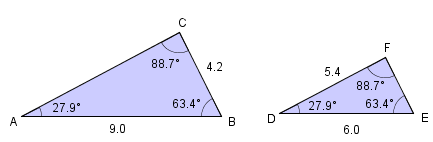
Her ser vi på korleis vi kan bruke formlikskap til å rekne ut ukjende sider i trekantar.
Opne i fag:
- Matematikk 1T-Y - SR
- Matematikk 1T-Y - FD
- Matematikk 1P-Y - BA
- Matematikk 1T-Y - EL
- Matematikk 1P-Y - DT
- Matematikk 1T
- Matematikk 1P-Y - FD
- Matematikk 1T-Y - HS
- Matematikk 1T-Y - BA
- Matematikk 1P-Y - NA
- Matematikk 1T-Y - TP
- Matematikk 1T-Y - NA
- Matematikk 1T-Y - DT
- Matematikk 1T-Y - IM
- Matematikk 1P-Y - EL
- Matematikk 1P-Y - IM
- Matematikk 1P-Y - TP
- Matematikk 1T-Y - RM