2.5.1
Gitt rektangelet nedenfor.
a) Regn ut arealet av rektangelet.
vis fasit
b) Regn ut lengden av diagonalen .
c) Regn ut arealet av trekanten .
vis fasit
Arealet av trekanten
d) Hva er arealet av trekanten ?
vis fasit
Trekantene og er formlike og like store.
Arealet av = Arealet av , altså
2.5.2
Gitt trapeset .
Finn arealet og omkretsen av trapeset.
vis fasit
Sidelengden .
Arealet av trapeset .
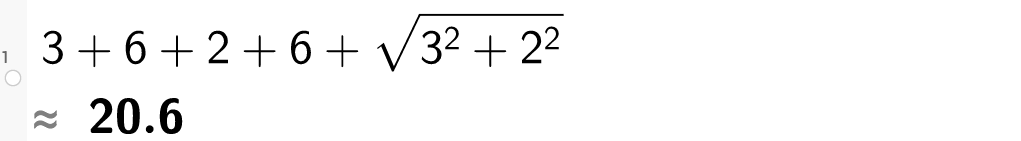
Finner omkretsen i GeoGebra:
Omkretsen av trapeset er .
2.5.3
Finn arealet av parallellogrammet .
vis fasit
Arealet av parallellogrammet
2.5.4
Regn ut arealet av trekanten .
vis fasit
Finner først høyden fra ned på linja gjennom .
Pytagoras´ læresetning gir:
Arealet av trekanten
2.5.5
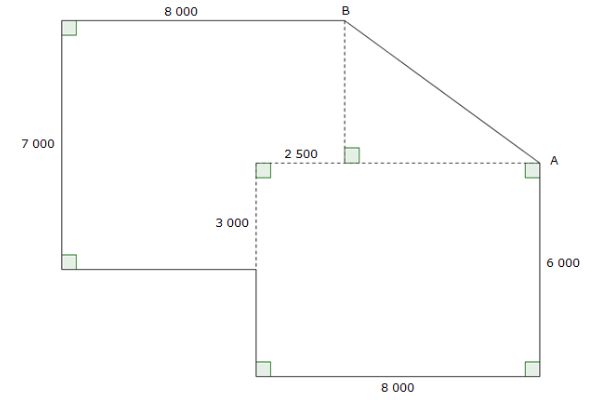
Stian skal sette opp et bygg. Grunnflaten har form som vist på tegningen ovenfor. Alle målene er gitt i millimeter (mm).
Vis at grunnflaten til bygget har et areal på .
vis fasit
Oppgaven kan løses på flere måter. Løsningen her er bare ett av mange alternativ.
Metode:
Finner arealet av de to store firkantene.
Legger til arealet av trekanten.
Trekker i fra det området der de to firkantene overlapper hverandre.
Areal av den øverste store firkanten .
Areal av den nederste store firkanten .
Areal av trekanten .
Areal av det området som blir med i begge de store firkantene .
Samlet areal blir: .
2.5.6
Figuren viser en likesidet trekant med sider . Utskjæringen er en halvsirkel med diameter .
a) Regn ut høyden i trekanten.
vis fasit
Trekanten er likesidet. Høyden treffer dermed midt på grunnlinjen.
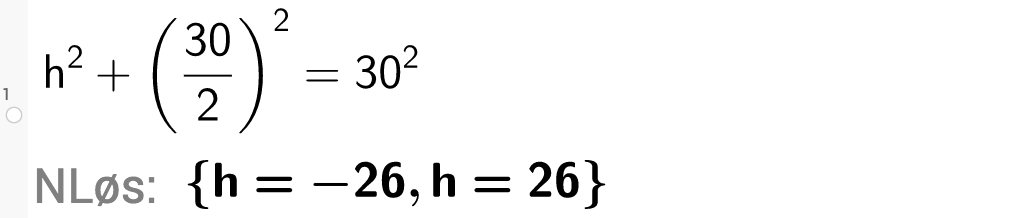
Løser i GeoGebra:
Høyden i trekanten er .
b) Regn ut arealet av den utskjærte trekanten.
vis fasit
Arealet av hele trekanten minus arealet av halvsirkelen.

Løser i GeoGebra:
Arealet er
c) Regn ut omkretsen av den utskjærte trekanten.
vis fasit
Omkretsen av halvsirkelen

Løser i GeoGebra:
Omkretsen av trekanten blir dermed:
2.5.7
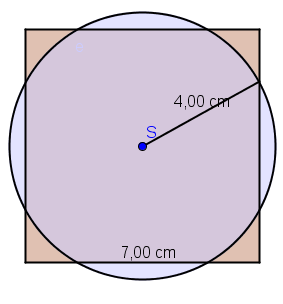
Hvilken figur har størst areal, en sirkel med radius 4,00 cm eller et kvadrat med sidelengde 7,00 cm?
vis fasit
Areal sirkel:

Løser i GeoGebra:
Areal kvadrat:
Arealet av sirkelen er størst.
2.5.8
Regn ut arealet av det lysegrå området på figuren.
vis fasit
Areal av rektangel:
Areal av de to kvartsirklene

Løser i GeoGebra:
Arealet av det lysegrå området blir:
